हां, आप सही हैं प्राइम का एल्गोरिदम डिजस्ट्रा के एल्गोरिदम की तरह काम करता है लेकिन प्राइम के एल्गोरिदम में इसे नकारात्मक किनारों वाले i से j तक के सबसे छोटे पथ की गणना नहीं करनी चाहिए। तो, उनका एक और एल्गोरिदम है जो कि बेलमैन-फोर्ड एल्गोरिदम है जो नकारात्मक किनारे के साथ i से j तक के सबसे छोटे पथ की गणना करता है।
प्राइम का एल्गोरिथम क्यों काम करता है?
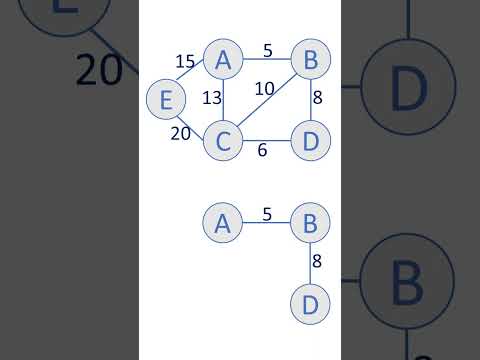
कंप्यूटर विज्ञान में, प्राइम का एल्गोरिथ्म (जर्निक के एल्गोरिथ्म के रूप में भी जाना जाता है) एक लालची एल्गोरिथ्म है जो एक भारित अप्रत्यक्ष ग्राफ के लिए न्यूनतम फैले हुए पेड़ को ढूंढता है इसका मतलब है कि यह एक सबसेट पाता है किनारे जो एक पेड़ बनाते हैं जिसमें प्रत्येक शीर्ष शामिल होता है, जहां पेड़ के सभी किनारों का कुल वजन कम से कम होता है।
क्या प्राइम का एल्गोरिथम सही है?
सटीकता का प्रमाण
हम साबित करते हैं कि प्राइम का एल्गोरिथ्म प्रेरण द्वारा सही है एल्गोरिथम द्वारा निर्मित बढ़ते पेड़ पर। … हम संकुचन द्वारा सिद्ध करते हैं कि Ti न्यूनतम फैले हुए वृक्ष का हिस्सा है। मान लें कि ei=(v, u) प्राइम के एल्गोरिथम द्वारा पाया गया किनारा है और मान लें कि यह न्यूनतम फैले हुए पेड़ का किनारा नहीं है।
प्राइम का एल्गोरिदम कितना कुशल है?
प्राइम का एल्गोरिथ्म कुशलता से काम करता है अगर हम सबसे सस्ते वज़न की सूची d[v] रखते हैं जो एक शीर्ष को जोड़ता है, v, जो पेड़ में नहीं है, पहले से ही किसी भी शीर्ष पर वृक्ष में। …
क्या प्रिम्स नेगेटिव वेट के साथ काम करती हैं?
क्या प्राइम है? समाधान: हां, दोनों एल्गोरिदम नकारात्मक बढ़त भार के साथ काम करते हैं क्योंकि कट संपत्ति अभी भी लागू होती है।